مقدمه
کوانت تریدینگ، رویکردی علمی و سیستماتیک برای فعالیت در بازارهای مالی است که بر پایه مدلهای ریاضی و آماری بنا شده است. موفقیت در این حوزه، صرفاً با تکیه بر شانس یا تحلیلهای ذهنی امکانپذیر نیست، بلکه نیازمند دانش عمیق علمی و درک ماهیت بازارهاست. برای دستیابی به کوانت تریدینگ و سپس الگوتریدینگ سودآور، باید بر دو زمینه کلی از دانش مسلط بود: درک قوانین و ماهیت بازارهای هدف و تسلط بر مفاهیم ریاضی و آماری.
در این مقاله به مرور دانش موردنیاز برای کوانت تریدینگ کوانت تریدینگ میپردازیم. اگر با مشاهده ویدئویهای آموزشی راحتترید، ویدئوهای زیر را به ترتیب ببینید. در این مقاله، به جهت پرهیز از طولانی شدن متن خلاصهسازیهایی انجام شده که ممکن است مفهوم موردنظر را برای شما کمی مبهم کرده باشد. اما در ویدئوها این طور نیست و موارد به تفصیل شرح داده شده است.
1) درک قوانین و ماهیت بازارهای هدف
2) انحراف معیار (Standard Deviation)
3) همبستگی (Correlation)
4) استنتاج آماری (Statistical Inference)
5) مانایی (Stationarity)
با این حال، اگر با متن راحتترید، به خواندن ادامه دهید!
ماهیت بازارها: روندی یا نوسانی؟
یکی از اولین گامها در طراحی استراتژیهای معاملاتی، درک ماهیت بازاری است که در آن فعالیت میکنید. آیا نمادها در این بازار تمایل به روندگیری دارند یا ماهیت آنها نوسانی و بازگشت به میانگین است؟. این ویژگی تأثیر بهسزایی بر نوع استراتژیهایی دارد که میتوانید تدوین کنید.
برای مثال، بازار فارکس به عنوان یک بازار بالغ، با حجم بالا و نقدینگی زیاد، ماهیتی عمدتاً نوسانی و بازگشت به میانگین دارد. قیمت جفتارزهایی مانند یورو/دلار آمریکا در یک دامنه مشخص نوسان میکند و شاهد تغییرات شدید و ناگهانی (مثلاً افت از ۱.۱ به ۰.۷ در عرض یک ماه) نیستیم. دلیل این امر، پایداری و قدرت اقتصادهای مرتبط با این ارزها و عدم اتخاذ تصمیمات ناگهانی و غیرمعمول است که اقتصاد آنها را زیر و رو کند.
در نقطه مقابل، بازار کریپتوکارنسی ماهیتی روندی و بعضاً انفجاری دارد. این بازار جوان، انقلابی، و ساختارشکن است. قیمت ارزها در آن میتواند طی یک هفته یا یک ماه دهها، صدها، هزاران یا حتی میلیونها برابر شود و سپس دوباره سقوط کند. این رفتار به دلیل نابالغ بودن بازار، جریان پول به سمت آن، و همچنین عدم رگولاسیون کافی است که امکان دستکاری قیمتها توسط عدهای را فراهم میکند. بنابراین، یک استراتژی روندگیر که روی کریپتو خوب عمل میکند، احتمالاً روی فارکس موفق نخواهد بود و بالعکس. این نکتهای بسیار مهم است که باید به آن توجه داشت.
ریسک و بازدهی در بازارها
مفهوم ریسک و بازدهی نیز ارتباط مستقیمی با ماهیت بازار دارد. به طور کلی، هرچه ریسک در یک بازار بیشتر باشد، بازدهی مورد انتظار نیز بیشتر خواهد بود. ریسک به معنی عدم قطعیت است و در بازارهای مالی، عدم قطعیت در بازدهی تعریف میشود.
در بازار کریپتو، به دلیل دامنه نوسان بسیار بالا و عدم قطعیت زیاد در مورد عملکرد آتی یک دارایی (مثلاً اینکه یک ارز فردا یا ماه آینده ۱۰٪ یا ۱۰۰۰٪ تغییر خواهد کرد)، ریسک فوقالعاده بالاست. در نتیجه، پتانسیل بازدهی نیز بسیار بالاست. این بازار خود به خود “اهرمدار” است و استفاده از اهرمهای معاملاتی (لوریج) در این بازار میتواند بسیار خطرناک و قمارگونه باشد.
در مقابل، در بازار فارکس به دلیل دامنه نوسان کمتر و عدم قطعیت پایینتر، بازدهی مورد انتظار نیز کمتر است. به همین دلیل است که بسیاری از معاملهگران فارکس از اهرم برای افزایش بازدهی استفاده میکنند، هرچند که این خود ریسک را افزایش میدهد.
ویژگیهای ذاتی دیگر بازارها مانند میزان نقدینگی و بلوغ بازار نیز مهم هستند. برای مثال، در بازار بورس ایران با دامنه نوسان محدود، پدیدههایی مانند صف خرید و فروش شکل میگیرند که میتوانند اجرای استراتژیهای معاملاتی (به خصوص استراتژیهای روندگیر) را تحت تأثیر قرار دهند. افزایش دامنه نوسان میتواند ساختار صفها را تغییر دهد و اثربخشی استراتژیهای قبلی را کاهش دهد. این نشان میدهد که استراتژیهای معاملاتی باید متناسب با ویژگیها و محدودیتهای ذاتی هر بازار طراحی شوند.
اهمیت ریاضیات و آمار به عنوان ستون فقرات کوانت تریدینگ
پس از درک ماهیت بازارها، ستون فقرات اصلی کوانت تریدینگ تسلط بر مفاهیم ریاضی و آماری است. این مفاهیم ابزارهایی قدرتمند برای تحلیل دادهها، مدلسازی ریسک و بازدهی، و استنتاج در مورد عملکرد آتی استراتژیها فراهم میکنند. شما باید این مفاهیم را در حد یک ریاضیدان درک کنید، نه صرفاً حفظ کنید.
دانش مورد نیاز در این زمینه را میتوان به سه سطح اصلی تقسیم کرد:
- آمار توصیفی (Descriptive Statistics): مفاهیمی مانند میانگین، میانه، مد، واریانس و انحراف معیار.
- استفاده از همبستگی (Correlation) برای سبدسازی (Portfolio Construction): درک رابطه خطی بین بازدهی داراییها یا استراتژیها.
- استنتاج آماری (Statistical Inference): توانایی استنباط در مورد جمعیت (آینده) بر اساس نمونه (گذشته).
یک سطح دیگر نیز وجود دارد که تحلیل سریهای زمانی و مانایی (Stationarity) است، اما تمرکز اصلی بر سه سطح اول است، زیرا ۹۵٪ فعالیتهای بیزینسی و پولسازی در کوانت تریدینگ با همین سه سطح قابل انجام است و ایدههای سودآور در این حوزه آنقدر زیادند که عمر یک شخص یا حتی یک سازمان برای بررسی همه آنها کافی نیست.
آمار توصیفی: کمیکردن ریسک و توصیف دادهها
مفاهیم آمار توصیفی، اگرچه ساده به نظر میرسند، اما اهمیت فوقالعادهای در تخمین رفتار آینده استراتژیها و سبد استراتژیها دارند.
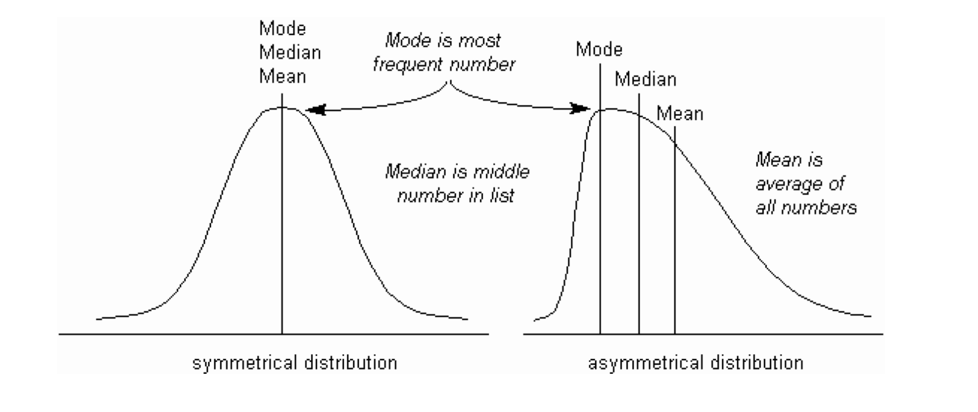
- میانگین (Mean)، میانه (Median)، و مد (Mode): این مفاهیم محل مرکز توزیع دادهها را نشان میدهند. درک رابطه میان این سه مقدار (مثلاً اینکه آیا بر هم منطبق هستند یا نه) میتواند اطلاعات مهمی در مورد شکل توزیع دادهها به ما بدهد.
- واریانس و انحراف معیار (Variance and Standard Deviation): این کمیتها بیانکننده پراکندگی نقاط داده از میانگینشان هستند. هرچه این عدد کوچکتر باشد، دادهها به میانگین نزدیکتر بوده و پراکندگی کمتر است. این مفاهیم به دو دلیل کلیدی برای ما اهمیت دارند:
- مدلسازی ریسک: انحراف معیار به طور مستقیم ریسک را کمّی میکند. انحراف معیار بازدهیهای یک دارایی یا استراتژی، نشاندهنده عدم قطعیت یا نوسان در آن بازدهیهاست. انحراف معیار کوچکتر به معنی نوسان کمتر در بازدهی و در نتیجه ریسک کمتر است. این مهمترین کاربرد انحراف معیار برای ماست.
- توصیف توزیع نرمال: در صورتی که دادهها دارای توزیع نرمال باشند (که شکل خاصی از هیستوگرام است که نسبت به میانگین متقارن است)، تنها با دانستن میانگین و انحراف معیار آن توزیع، میتوانیم کل مجموعه دادهها را توصیف کنیم. توزیع نرمال ویژگیهای ریاضی خاصی دارد و در آن، میانگین، میانه و مد بر هم منطبق هستند. در یک توزیع نرمال، میتوان با احتمال مشخصی (مثلاً حدود ۶۸.۲٪) گفت که بازدهی آینده در فاصله مثبت و منفی یک انحراف معیار از میانگین قرار خواهد گرفت.
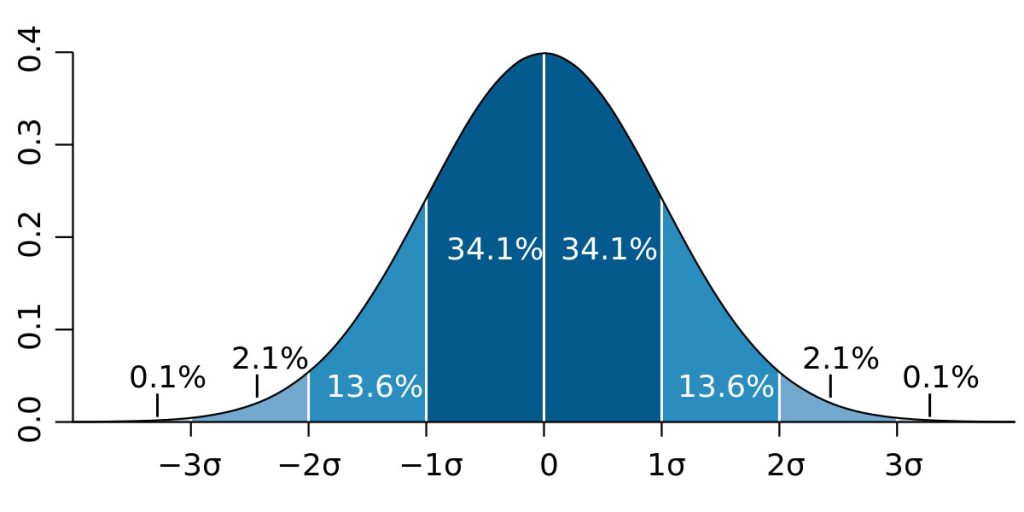
هیستوگرام یک نمایش بصری از توزیع دادهها است که با تقسیم دامنه تغییرات دادهها به بازههایی (مثلاً بازههای قد افراد) و شمارش تعداد دادهها در هر بازه ساخته میشود. با این حال، بازدهی خام یک نماد یا استراتژی معمولاً مستقیماً به توزیع نرمال نمیرسد. اما همانطور که در بخش استنتاج آماری خواهیم دید، روش خاصی وجود دارد که میتوانیم به توزیع نرمال در بازدهیها دست یابیم و از آن برای استنباط آماری استفاده کنیم.
همبستگی: قلب سبدسازی موفق
همبستگی (Correlation) بیانکننده وجود یا عدم وجود رابطه خطی بین دو متغیر آماری است. ضریب همبستگی مقداری بین منفی ۱ تا مثبت ۱ دارد.
- همبستگی نزدیک به مثبت ۱: نشاندهنده رابطه خطی مستقیم قوی است. به این معنی که با افزایش یک متغیر، متغیر دیگر نیز تمایل به افزایش دارد (مثلاً اگر بازدهی کوین A مثبت باشد، بازدهی کوین B نیز مثبت است).
- همبستگی نزدیک به منفی ۱: نشاندهنده رابطه خطی معکوس قوی است. به این معنی که با افزایش یک متغیر، متغیر دیگر تمایل به کاهش دارد (مثلاً اگر بازدهی کوین A مثبت باشد، بازدهی کوین B منفی است).
- همبستگی نزدیک به صفر: نشاندهنده عدم وجود رابطه خطی قابل ملاحظه بین دو متغیر است. به این معنی که وقتی یک متغیر مثبت است، متغیر دیگر ممکن است مثبت یا منفی باشد و از نظر آماری نمیتوان ارتباط مستدلی بین آنها یافت.
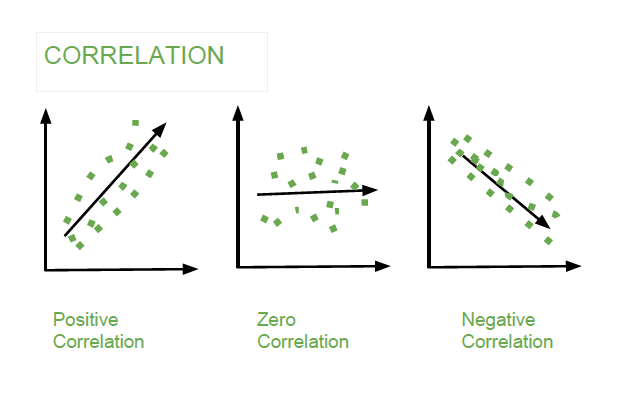
در ترید و سرمایهگذاری، ما از حالتهای همبستگی بالا (چه مثبت چه منفی) گریزانیم و حالت جذاب برای ما وقتی است که همبستگی بین بازدهیها نزدیک به صفر باشد. این مفهوم، رأس دوم مثلث طلایی الگوتریدینگ است. مثلث طلایی شامل: ۱. استراتژیهای تکبهتک سودآور، ۲. سبدسازی به شکلی که همبستگی بازدهی استراتژیها پایین باشد (در حالت ایدهآل بین مثبت و منفی ۰.۳)، و ۳. اطمینان از سودآوری استراتژیها در آینده.
چرا همبستگی پایین مهم است؟
وقتی استراتژیهای سودآور را با همبستگی پایین در یک سبد قرار میدهیم، سود آنها جمع میشود و ضررهایشان همدیگر را خنثی میکنند. استفاده از ابزارهای شبیهساز سبد سرمایهگذاری میتواند اثر همبستگی بر عملکرد سبد را به وضوح نشان دهد. در یک شبیهسازی با ۱۰ استراتژی، مشاهده میشود که با کاهش همبستگی بین بازدهی استراتژیها، عملکرد کلی سبد به طور قابل توجهی بهبود مییابد.
معیار مهم در این زمینه، شارپ ریشیو (Sharpe Ratio) است. شارپ ریشیو به نوعی سودآوری تعدیلشده بر حسب ریسک را نشان میدهد؛ هرچه بالاتر باشد بهتر است. با کاهش همبستگی (مثلاً از ۰.۹ به ۰.۷۵، ۰.۵ و سپس ۰.۳)، مشاهده میشود که شارپ ریشیو سبد افزایش یافته و همزمان حداکثر افت سرمایه (Drawdown) کاهش مییابد. این نتیجه سبدسازی درست است (استراتژیهای سودآور با همبستگی پایین) که باعث میشود بازدهی سبد بالاتر از تک تک استراتژیها باشد و ریسک سبد از آنها کمتر باشد.
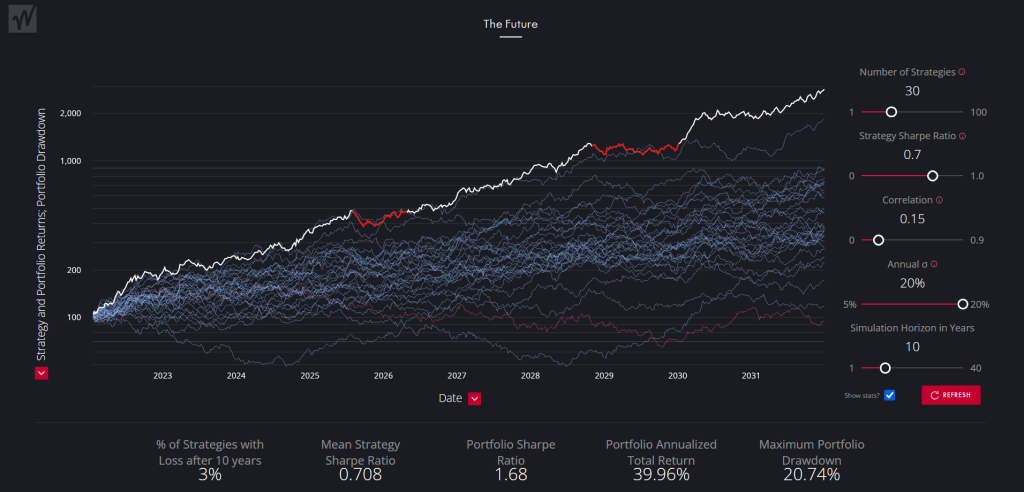
نکته مهم: صرفاً خرید و نگهداری (Buy and Hold) مجموعهای از کوینها در بازار کریپتو، سبدسازی واقعی محسوب نمیشود. دلیل آن همبستگی فوقالعاده بالای بازدهی کوینها در بازار کریپتو است (مثلاً همبستگی بیتکوین و اتریوم حدود ۰.۸۰-۰.۸۵ است). وقتی بازار سقوط میکند، همه کوینها با هم سقوط میکنند و وقتی صعودی میشود، همه با هم صعود میکنند. در چنین شرایطی، شما عملاً ریسک خود را افزایش دادهاید، نه اینکه آن را مدیریت کرده باشید.
هدف این است که استراتژیهایی انتخاب شوند که بازدهیهای آنها در طول زمان همبستگی پایینی داشته باشند.
دستیابی به همبستگی پایین بین استراتژیها کار سختی نیست. با انتخاب استراتژیهایی که همبستگی پایینی دارند و قرار دادن آنها در یک سبد، میتوان به منحنی سرمایه (Equity Curve) بسیار هموارتر و با ثباتتری رسید. این همان چیزی است که یک بیزینس در کوانت تریدینگ به دنبال آن است و میتواند منجر به بازدهیهای قابل توجهی در بلندمدت شود (مثلاً ۱۰۰ برابر شدن سرمایه اولیه در ۱۰ سال در یک شبیهسازی با استراتژیهای دارای شارپ ریشیو معمولی و همبستگی پایین).
این نتایج حتی روی دادههای تصادفی نیز قابل مشاهده است. افزایش تعداد استراتژیهای غیرهمبسته در سبد (طبق قانون بنیادی مدیریت فعال) نیز میتواند به بهبود عملکرد سبد کمک کند، اما این مزیت تا حدی ادامه دارد و پس از آن، معیارها تغییر چندانی نمیکنند.
استنتاج آماری: تخمین سودآوری در آینده
مهمترین “اما و اگر” در مثلث طلایی، اطمینان از سودآوری استراتژیها در آینده است. کسی نمیتواند آینده را پیشبینی کند. اما با کمک علم آمار میتوان با احتمال بالا در مورد رفتار آتی استراتژیها استنتاج کرد. اینجاست که استنتاج آماری وارد میشود.
یکی از روشهای علمی برای ارزیابی پتانسیل سودآوری یک استراتژی در آینده، روش اثبات معکوس (Proof by Contradiction) است. اساس این روش بر این است که یک فرض اولیه و مخالف آنچه میخواهیم اثبات کنیم را در نظر میگیریم، و سپس سعی میکنیم این فرض را نقض کنیم.
اثبات معکوس و فرض اولیه (Null Hypothesis)
در مورد استراتژی معاملاتی، فرض اولیه ما (Null Hypothesis) این است که استراتژی سودآور نیست. این فرض پایهای امنتر و محتملتر برای شروع است. ما میخواهیم خلاف این را ثابت کنیم.
برای این کار، میتوانیم عملکرد استراتژی مورد نظر خود را با عملکرد تعداد زیادی استراتژی کاملاً تصادفی که هیچ منطق موجهی ندارد مقایسه کنیم. یک استراتژی غیرسودآور، استراتژیای است که هیچ منطق معاملاتی پشت آن نیست و اگر نتیجه خوبی گرفته، صرفاً شانس آورده است. میتوان با شبیهسازی خرید و فروش تصادفی (مثلاً با انداختن سکه برای ورود یا خروج در هر کندل)، تعداد زیادی (مثلاً ۱۰ هزار) از این استراتژیهای تصادفی را مدل کرد. این کار روی دادههای تاریخی مشخصی انجام میشود، مثلاً دادههای روزانه بیتکوین در بازهای خاص (از ابتدای ۲۰۱۸ تا پایان ۲۰۲۰). انتخاب بازه داده با حداقل تعداد کندل (مثلاً ۱۰۰۰ کندل) مهم است تا نتایج محاسبات آماری همگرا شوند.
قضیه حد میانی (Central Limit Theorem)
برای مقایسه استراتژی تصادفی، میتوان از میانگین بازدهی کندلی هر استراتژی استفاده کرد. دلیل استفاده از میانگین بازدهی کندلی و نه معیار دیگری مانند Net Profit یا Sharpe Ratio، قضیه حد میانی (Central Limit Theorem) در ریاضیات است. این قضیه بیان میکند که اگر از مجموعهای از متغیرهای تصادفی مستقل میانگین بگیریم، توزیع این میانگینها تمایل به توزیع نرمال خواهد داشت. این دقیقاً همان چیزی است که ما به دنبال آن هستیم: یک توزیع نرمال که بتواند ۱۰۰٪ دادهها را توصیف کند، هم در گذشته و هم در آینده!
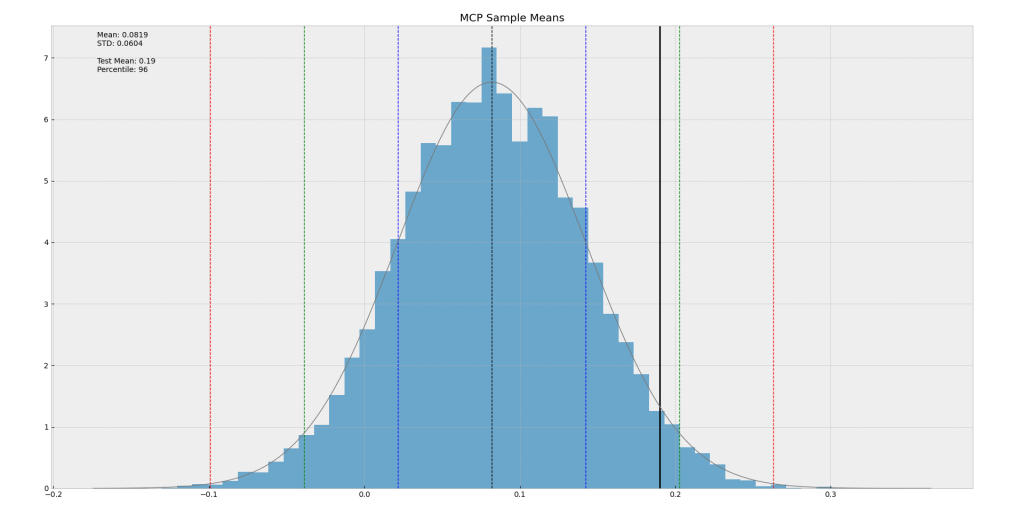
وقتی میانگین بازدهی کندلی ۱۰ هزار استراتژی تصادفی را محاسبه کرده و هیستوگرام آن را رسم کنیم، به توزیعی میرسیم که به توزیع نرمال میل میکند و با افزایش تعداد نمونهها (بکتستها) کاملاً نرمال میشود. این هیستوگرام، توزیع سود تصادفی و شانسی را روی بازه زمانی مورد نظر نشان میدهد. در مثال ارائه شده، میانگین بازدهی کندلی ۱۰ هزار استراتژی تصادفی حدود ۰.۰۸٪ در روز بوده است. این نکته جالب نشان میدهد که حتی با ترید تصادفی در بازار رو به رشد و نابالغی مانند کریپتو (در آن بازه زمانی که بازار U شکل را تجربه کرد)، میانگین بازدهی صفر نبوده است؛ این میتواند هم نشانه فرصت سودآوری آسان در بازار باشد، و هم هشداری باشد که نتایج خوب در فاز صعودی بازار ممکن است صرفاً ناشی از شانس باشد.
پذیرش یا رد فرض اولیه
اکنون، میانگین بازدهی کندلی استراتژی مورد نظر خودمان را که میخواهیم آن را ارزیابی کنیم (که در این مرحله نباید روی آن هیچ بهینهسازی یا Optimization انجام شده باشد تا نتیجه صادقانه باشد)، روی این هیستوگرام توزیع تصادفی قرار میدهیم. در مثال منابع، میانگین بازدهی کندلی استراتژی مورد نظر حدود ۰.۱۹٪ در روز بوده است. این عدد در کجای توزیع تصادفی قرار میگیرد؟ این عدد، صدک ۹۶ام (96th Percentile) توزیع تصادفی را تشکیل میدهد.
این به چه معنی است؟ معنی این است که ۹۶ درصد از آن ۱۰ هزار استراتژی تصادفی، نتایجی بدتر از استراتژی ما داشتهاند. با توجه به فرض اولیه (Null Hypothesis) که استراتژی سودآور نیست و این هیستوگرام نشاندهنده توزیع نتایج شانسی است، این نتیجه (قرار گرفتن در صدک ۹۶) به ما میگوید که به احتمال حداکثر ۴٪ (۱۰۰٪ – ۹۶٪)، استراتژی ما صرفاً شانس آورده که این نتایج را کسب کرده است. نقطه مقابل این استنتاج این است که به احتمال حداقل ۹۶٪، استراتژی ما دارای یک “قدرت پیشبینی” (Prediction Power) واقعی بوده است که به این نتایج رسیده است.
آستانه پذیرش (Significance Level)
این احتمال حداکثر ۴٪، با مفهوم پی ولیو (p-value) در آمار مرتبط است. پی ولیو در واقع احتمال مشاهده نتایج به این خوبی یا بهتر از آن، با فرض درست بودن فرض صفر (استراتژی سودآور نیست) است. ما میتوانیم یک آستانه پذیرش (Significance Level) برای پی ولیو در نظر بگیریم. برای مثال، در بازارهای سرمایه که عدم قطعیت بالاست، ممکن است آستانه ۰.۰۵ (یا ۵٪) را در نظر بگیریم. این به این معنی است که ما میپذیریم حداکثر ۵٪ احتمال خوششانسی وجود داشته باشد. برای اینکه یک استراتژی از نظر آماری معنادار و احتمالا سودآور در آینده تلقی شود، باید از حداقل ۹۵٪ نتایج استراتژیهای تصادفی بهتر عمل کند. در مثال ما، استراتژی با قرار گرفتن در صدک ۹۶، از ۹۶٪ نتایج تصادفی بهتر عمل کرده است. این عدد (۹۶٪) از آستانه ۹۵٪ بالاتر است، بنابراین میتوانیم فرض صفر (استراتژی سودآور نیست) را رد کرده و بپذیریم که استراتژی دارای قدرت پیشبینی واقعی است و احتمالاً در آینده نیز سودآور خواهد بود.
میتوان آستانه پی ولیو را سختگیرانهتر (مثلاً ۰.۰۱ یا ۱٪) یا آسانتر (مثلاً ۰.۱۰ یا ۱۰٪) انتخاب کرد. در کارهای پزشکی که قطعیت بسیار بالایی نیاز است، ممکن است پی ولیو ۱٪ یا حتی ۰.۱٪ مد نظر قرار گیرد. دستیابی به پی ولیو پایینتر نشاندهنده اطمینان بیشتر است، اما بسیار دشوار است، به خصوص اگر ایده اولیه خام و بدون بهینهسازی باشد.
انجام این تست آماری و رسیدن به نتیجهای مانند صدک ۹۶، اطمینان زیادی در مورد آینده استراتژی به ما میدهد.
نکته حیاتی اینجاست که این تست باید روی ایده خام و اولیه استراتژی انجام شود و نباید هیچگونه بهینهسازیای روی آن صورت گرفته باشد.
بهینهسازی استراتژی قبل از این تست، “سر خود کلاه گذاشتن” است و نتایج تست را بیاعتبار میکند. اگر استراتژی خام در این تست آماری موفق شود و قدرت پیشبینی آن ثابت شود، آنگاه ارزش آن را دارد که زمان و انرژی باارزش و محدود خود را صرف آن ایده کنیم و با اضافه کردن مدیریت ریسک، مدیریت سرمایه و بهینهسازی، سعی کنیم استراتژی کامل و قابل استفادهای را براساس آن ایده تدوین کنیم.
یادگیری ماشین: ابزاری قدرتمند، اما نیازمند دانش پایه
برخی ممکن است فکر کنند با ظهور یادگیری ماشین (Machine Learning – ML)، دیگر نیازی به درک عمیق مفاهیم ریاضی و آماری نیست و میتوان صرفاً به ماشین گفت که در بازار به دنبال سود بگردد. اما اینطور نیست. یادگیری ماشین زیرمجموعهای از هوش مصنوعی است که از فرایند یادگیری ذهن انسان الگو گرفته است.
در استراتژیهای معاملاتی “کلاسیک” (به معنی غیر ML)، هسته تصمیمگیری (مثلاً استفاده از یک اندیکاتور خاص با پارامترهای ثابت و شرایط ورود و خروج مشخص) به طور صریح کدنویسی میشود. در یادگیری ماشین، ما یک مدل میسازیم که به شکل صریح کدنویسی نشده، بلکه با آموزش (Training) بر روی دادهها، یاد میگیرد که چگونه تصمیمگیری کند.
اما یادگیری ماشین صرفاً یک ابزار است. اصل مهم “Garbage In, Garbage Out” (آشغال بده، آشغال بگیر) در اینجا کاملاً صدق میکند. اگر دادههای ورودی (Features) که برای آموزش مدل ML استفاده میشوند، بیارزش باشند، خروجی مدل نیز بیارزش خواهد بود.
یکی از مفاهیم کلیدی که به شناسایی دادههای ورودی مفید برای مدلهای ML کمک میکند، بحث مانایی (Stationarity) است. به بیان ساده، یک متغیر آماری مانا است اگر میانگین و واریانس آن در گذر زمان ثابت باشد. اگر یک فیچر (ورودی مدل ML) مانا نباشد، قطعاً یک “آشغال” است. با این حال، مانا بودن یک فیچر لزوماً به معنی مفید بودن آن نیست.
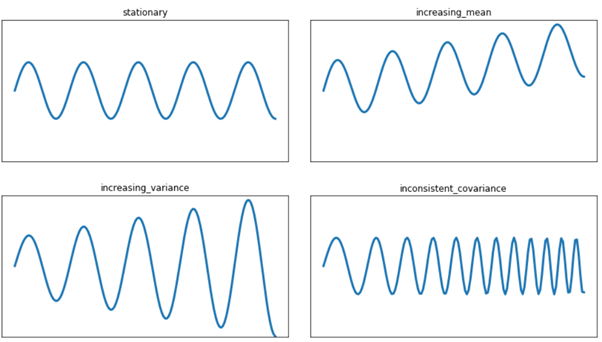
ناقضهای مانایی شامل مواردی مانند میانگین افزایشی، واریانس افزایشی یا کاهشی، و یا تغییرات در دامنه نوسان در طول زمان هستند. حتی برای ارزیابی مانایی در دادههای گذشته، باز هم به مفاهیم میانگین و انحراف معیار (واریانس) نیاز داریم.
مهمتر از همه، ارزیابی مانایی روی دادههای گذشته انجام میشود و ما از آینده خبر نداریم.
بنابراین، همچنان با چالش استنتاج از گذشته به آینده روبرو هستیم. دستیابی به فیچرهای مانا در گذشته و آینده، نیازمند درک عمیق همان مفاهیم ریاضی و آماری پایهای است. حتی خروجی یک اندیکاتور ساده به راحتی نمیتواند یک فیچر مناسب برای مدل ML باشد؛ رسیدن به فیچرهای مفید نیازمند پردازشهای پیچیدهتر است که بر همان مفاهیم ریاضی استوار است.
نتیجهگیری: فقط یک راه وجود دارد و آن هم سخت است!
در نهایت، چه هدف شما صرفاً پول درآوردن بدون تعصب باشد و چه علاقهمند به استفاده از ابزارهای پیشرفته مانند یادگیری ماشین باشید، هیچ راه میانبری وجود ندارد. شما باید مفاهیم اساسی ریاضی و آماری مانند میانگین، انحراف معیار، همبستگی و استنتاج آماری را درک کنید. این دانش به شما امکان میدهد تا:
- ماهیت بازارهای هدف خود را بشناسید و استراتژیهای متناسب تدوین کنید.
- ریسک استراتژیهای خود را کمی کرده و مدیریت کنید.
- با سبدسازی علمی بر پایه همبستگی پایین، عملکرد کلی سرمایهگذاری خود را بهبود بخشید، ریسک را کاهش داده و بازدهی را افزایش دهید.
- با استفاده از استنتاج آماری و تستهای معناداری، پتانسیل سودآوری استراتژیهای خود در آینده را با احتمال بالا تخمین بزنید.
- حتی در استفاده از ابزارهای پیشرفته مانند یادگیری ماشین، دادههای ورودی باکیفیت را شناسایی کرده و از اصل “Garbage In, Garbage Out” در امان باشید.
این سه رأس مثلث طلایی (استراتژیهای سودآور فردی، سبدسازی با همبستگی پایین، و اطمینان از سودآوری آتی بر پایه استنتاج آماری)، همان راهکار و نقشه گنجی است که در بازارهای سرمایه منجر به موفقیت پایدار میشوند. با تکیه بر این دانش علمی، میتوان به “قطعیت بیزینسی” مورد نیاز دست یافت و از حدس و گمان و شانس فراتر رفت.
این مسیر نیازمند یادگیری عمیق و مداوم است. اما پتانسیل بازدهی و ثبات در فعالیت حرفهای، ارزش این سرمایهگذاری را دارد.
⭐️ محتوای این مطلب از دوره آموزشی مبانی و مفاهیم کوانت تریدینگ و الگوتریدینگ اقتباس شده است. ⭐️
〰️〰️〰️〰️〰️
🔵🔵🔵 همین حالا در دوره رایگان مبانی و مفاهیم کوانت تریدینگ و الگوتریدینگ ثبت نام کنید! 🔵🔵🔵
🔴🔴🔴 در کانال یوتیوب الگویو عضو شوید و بخشهای رایگان سایر دورهها را مشاهده کنید! 🔴🔴🔴
🟢🟢🟢 در بحث و تبادل نظر تخصصی درباره این دوره شرکت کنید! 🟢🟢🟢
〰️〰️〰️〰️〰️